• Introduction
• Examples
• Limitations
• References and further resources
• Appendix
• Footnotes

Introduction

Ever since I heard about those things called “continuations”, I’ve been fascinated by what they are and how they work, specially after discovering this thing called callCC^{1 2}. If this was not hard enough to grasp, some time later I discovered that continuations can be delimited or undelimited. Recently I found several references about continuations³, but they tend to be papers that are hard to read without some prior knowledge, which I don’t have. Therefore, I’m unable to present here some intuitive explanation about them. Maybe after much more reading.

Instead, this post is about a proof of concept (POC) delimited continuations library in Elixir. This is the result of my attempts at trying to understand (delimited) continuations by way of practice. The resulting library converts Elixir code into continuation passing style, and then uses that transformed code to implement the control operators shift and reset. Theses things will be briefly discussed here. I hope this may help someone else trying to grasp continuations and, if I’m lucky, someone may teach me more by pointing out the gaps in my understanding and implementation. =)

This post presents some (hopefully) interesting examples of what can be done using those operators. A very simplistic (and perhaps erroneous, as I’m still grasping those concepts… beware!) explanation of what I gathered so far about this topic and a few implementation details I stumbled upon are presented in the appendix. The implementation is available on Github.

Examples

Here, I’ll present the basic usage of the library and some examples. For more on CPS and shift/reset, see the corresponding sections. Several examples will slowly build over one another because I found it interesting to do so when I was trying to grasp the concepts myself gradually.

The experimental library is Campinas⁴, available on Github. To use it, just add use Campinas at the beginning of your module, define functions to be CPSed using the defcps/2 macro and run them using the runCPS/1 macro. Notice that the current implementation is pretty much a POC, so several AST nodes are not yet supported, such as pipes, for/1, receive/after blocks and many others.

The most basic example is one where nothing fancy is done:

defmodule Example do
  use Campinas

  defcps ex1(x) do
    y = x + 1
    z = 2 * y - 3
    div(z, 3)
  end
end

Running runCPS(Example.ex1(10)) gives 6, as expected.

Things start to get a bit more interesting when we introduce shift/reset. I’ll give a few very basic examples with growing complexity to try to demonstrate how those work intuitively. First, using just reset basically does nothing by itself:

defcps ex2() do
  x = reset do
        4
      end
  x + 1
end

runCPS(Example.ex2()) results in 5, as if reset wasn’t there. Similarly, an expression using only shift appears to have no visible effects as well (cont is the name we give our continuation; it can be something else as well):

defcps ex3() do
  shift cont do
    6
  end
end

runCPS(Example.ex3()) indeed results in 6. The first strange example is one where we use shift in a more complex expression. Let’s take ex1 and use shift in its second expression:

defcps ex4(x) do
  y = x + 1
  z = 2 * shift cont do
            99
          end - 3
  div(z, 3)
end

If shift were truly a no-op, one would expect runCPS(Example.ex4(10)) to yield 65. Yet, the final result is 99! It is as if invoking shift acts like an early function exit such as return from a more imperative language. Notice that we didn’t invoke the continuation inside shift. If we do that:

defcps ex5(x) do
  y = x + 1
  z = 2 * shift k do  # also changed the name, for fun
            k(99)     # here we invoke the captured continuation
          end - 3
  div(z, 3)
end

… then, indeed, runCPS(Example.ex5(10)) yields 65. But what if we do more than simply invoking the continuation inside shift?

defcps ex6(x) do
  y = x + 1
  z = 2 * shift k do
            k(99) - 60
          end - 3
  div(z, 3)
end

This results in 5! In effect, it is the same as ex4, but with 60 subtracted from it. Essentially, when we invoke shift, the whole function result is shift’s body. In this example, the continuation is a function that is roughly equivalent to fn v -> div(2 * v - 3, 3) end.

That behavior is changed when we add reset to the mix. It effectively delimits the extent to which shift can capture the continuation.

defcps ex7(x) do
  y = x + 1
  z = reset do
        2 * shift cont do
              cont(99) - 60
            end
      end - 3
  div(z, 3)
end

The result now is 45. The captured continuation is now equivalent to fn v -> 2 * v end because of the enclosing reset. Another interesting thing is that the continuation may be invoke more than once. The following example results in 13:

defcps ex8() do
  z = reset do
        2 * shift cont do
              cont(cont(8)) + 11
            end
      end - 3
  div(z, 3)
end

Multiple CPSed functions that use shift and reset can be composed using the ad-hoc syntax @[expression]. We can break up ex8 into two smaller functions, and has the same behavior as before:

defcps ex9() do
  shift cont do
    cont(cont(8)) + 11
  end
end

defcps ex10() do
  z = reset do
        2 * @[ex9()]
      end - 3
  div(z, 3)
end

We can also shift inside of a tuple literal:

defcps ex11() do
  {
    1,
    2,
    shift cont do
      Tuple.to_list(cont(99))
    end,
    4
  }
end

This results in [1, 2, 99, 4].

A more bizarre example taken from one of the original papers that introduce shift/reset⁵ is one that writes seemingly direct code to compute “non-deterministically” combinations of numbers that add up to a given value. We need to define a few functions that do the magic:

@doc "aborts the computation early"
defcps fail() do
  shift k do
    :no
  end
end

@doc "tries to continue with both true and false"
defcps flip() do
  shift k do
    k(true)
    k(false)
    @[fail()]
  end
end

@doc "continues with all numbers below a maximum"
defcps choice(n) do
  # by the way, `if` is supported
  if n < 1 do
    @[fail()]
  else
    if @[flip()] do
      @[choice(n - 1)]
    else
      n
    end
  end
end

@doc """
tries to find all x > y > z with x <= n such that x + y + z = s
"""
defcps triples(n, s) do
  x = @[choice(n)]
  y = @[choice(x - 1)]
  z = @[choice(y - 1)]

  if x + y + z == s do
    send(self(), {:found, {x, y, z}})
  else
    @[fail()]
  end
end

Then, to find such triples with n = 9 and s = 15:

defcps ex12() do
  @[triples(9, 15)]
end

Running this yields:

iex(201)> runCPS(Example.ex12())
:no
iex(202)> flush()
{:found, {6, 5, 4}}
{:found, {7, 5, 3}}
{:found, {7, 6, 2}}
{:found, {8, 4, 3}}
{:found, {8, 5, 2}}
{:found, {8, 6, 1}}
{:found, {9, 4, 2}}
{:found, {9, 5, 1}}
:ok
iex(203)>

Effect systems

As the final example, I’ll show simple error and state effects built upon those operators. It has been observed that delimited continuations can be used to model effect systems^{6 7}.

The simplest one is the error effect. Reminding ourselves of example ex4, an early exit would be implemented as simply as calling shift. To add extra spice, we’ll consider recoverable exceptions: the user provides a handler that receives the error e and decides if computation should halt and return {:error, e}, or if it should continue (and provide a value back to the computation).

 # the program
defmodule ErrorExample do
  use Campinas
  alias Campinas.Effects.Error

  defcps program1(x) do
    y = x * x - 1

    if y < 0 do
      @[Error.error(:negative)]
    end

    result =
    if y > 100 do
      @[Error.error({:too_big, y})]
    else
      div(y, 2)
    end

    result - 1
  end
end

# the usage
handler = fn
  {:too_big, n} ->
    send(self(), {:big_number, n})

  if rem(n, 2) == 0 do
    {:cont, 0}
  else
    :halt
  end

  e ->
    send(self(), {:some_error, e})
  :halt
end

run_error(ErrorExample.program1(2), handler)
# should return `{:ok, 0}` without calling the handler

run_error(ErrorExample.program1(11), handler)
# should return `{:ok, -1}` and call the handler, which continues

run_error(ErrorExample.program1(0), handler)
# returns `{:error, :negative}` and call the handler, which aborts

The state effect is our last example. It has two operations: get/0, which simply reads the current state, and set/1, which defines a new state. The stateful program is run by being fed to run_state/2 along with the initial state. This returns {:ok, result, final_state}.

# the program
defmodule StateExample do
  use Campinas
  alias Campinas.Effects.State

  defcps program1(x) do
    s1 = @[State.get()]
    s2 = x + s1

    if rem(s2, 2) == 0 do
      @[State.set(s2 + 11)]
    else
      @[State.set(4 * s2)]
    end

    2 * s2 + 1
  end
end

# the usage
run_state(StateCases.program1(11), 20)
# returns `{:ok, 63, 124}`; 63 is the result; 124 is the final state

run_state(StateCases.program1(10), 20)
# returns `{:ok, 61, 41}`; 61 is the result; 41 is the final state

Notice that there is no mutation involved, nor exceptions being raised/thrown (in the Elixir/Erlang sense) in those examples. ;)

Limitations

I have not implemented several AST node possibilities in the transformation, so almost anything outside the examples in the tests will probably not work. =)

The example from the composable-continuation tutorial on the Scheme Wiki does not work with the current version. I believe that Enum.each (the equivalent of for-each there) would need to be CPSed for that to work.

References and further resources

Here are some resources I have used, not necessarily in their entirety, and others that I have found while researching this topic.

• Delimited Continuations for Everyone by Kenichi Asai (Youtube)

  Nice video explaining delimited continuations with examples. It is also where I found some recommendations of further resources (around 01:30).

• Olivier Danvy and Andre Filinski, “Representing Control: a Study of the CPS Transformation”, MSCS, 1992

  The introductory paper recommended by Kenichi Asai. It does seem to have some prior knowledge assumptions, but seems very comprehensive and has very helpful tables of conversion rules for CPSing programs.

• Olivier Danvy and Andre Filinski, “Abstracting Control,” LISP and Functional Programming, 1990

  Another earlier paper by the authors who introduced shift and reset. It is more compact, has a couple examples, but is much more dense and harder to understand (much more assumed knowledge about concepts and notation).

• Racket Reference Manual on Continuations

  Great source of references and displays other control operators. Not quite didactic, but I recommend browsing it and trying out the operators, since the implementation is solid in Racket.

• Composable Continuations Tutorial on Scheme Wiki

  A nice and short tutorial with some examples that are very illuminating examples that are valuable to be worked out manually.

• delimc by David Nolen

  A delimited continuations library for Clojure. Nice and short implementation to study.

• The proposal to add delimited control primops to GHC and a companion email thread

  Low level discussion of adding control operators similar to shift and reset to GHC, and how these affect the execution stack.

• This answer to a StackOverflow question about continuation prompts by Alexis King

  Has some nice visualizations relating stack frames and delimited continuations.

• guile and delimited continuations, by Andy Wingo

  One of the implementers of GNU Guile (a Scheme implementation) discusses adding delimited continuations to the language. Has some nice illustrations of the stack for the control/prompt operators (cousins of shift/reset).

• rain-1’s continuation study group

  A vast collection of papers and references about continuations in general. It’ll take quite a while to chew through all that. =)

  I’d love to know if this group has a forum or similar channel where one could ask questions.

Appendix

Continuation Passing Style (CPS)

This sections describes briefly what CPS is and some decisions that I had to make in the implementation in order for it to work. Although I’m still making sense of them 🙈.

A continuation is the materialization of “what comes next” at a given point of execution of a program. Or, a continuation is the evaluation context surrounding the reducible expression (redex)⁸. Using the same example from the Racket documentation:

#  continuation
# ↓↓↓↓
  4 - (1 + 1)
#     ↑↑↑↑↑↑↑
#      redex

Here, in order for the whole expression to be reduced, the redex is (1 + 1), and the continuation is 4 - _, where _ takes the place of the redex as it is reduced. As another example:

def some_fun() do
  x = 1      # the lines below are this expression's continuation.
  y = x + 2  # `x` is the "redex" that is fed here, and `_ + 3` is
             # this line's continuation.
  y + 3      # within this line, `_ + 3` is `y`'s continuation
end

Continuation Passing Style (CPS) is a way of writing functions and expressions where the continuation is passed as an explicit argument to the redex.

Irreducible values

The simplest case is that of a value that cannot be reduced further. Using the notation⁹ [[ E ]] to denote the CPS conversion of a term E, the conversion of a pure value is simply:

[[ x ]] = λκ. κ x

In Elixir:

# a simple value...
1
# ... in CPS form becomes:
fn k -> # `k` is the continuation, to be provided by some other code.
  k.(1) # that continuation is invoked and receives the value to
        # proceed.
end

Primitive function application

Another simple case is that of primitive function application. A primitive function is one that is considered a “black box” and its definition cannot be directly converted into CPS. I considered local and remote function calls as primitives.

For a primitive function p applied to x, its conversion rule is:

[[ p x ]] = λκ. [[ x ]] (λa. κ (p a))

Let’s take as an example the negate unary operator, Kernel.-/1.

- x
# ... in CPS form becomes:
fn k1 ->         # the outer continuation
  (fn k2 ->      # ─┐ this `k2` is the lambda defined below
    k2.(x)       #  │
  end).(fn a ->  # <┘
                 # the outer continuation receives the result of the
    k1.(- a)     # primitive function application
  end)
end

If you manually evaluate the above expression, you’ll see that it is indeed equivalent to the original expression.

If there are multiple arguments, we first have to curry¹⁰ the function before converting. This is the default behavior in a few languages such as Haskell and OCaml, but is a bit unusual in Elixir. If we start with the following for Kernel.-/2:

fn x, y ->
  x - y
end

The curried form (not yet “CPSed”), is equivalent to:

fn x ->
  fn y ->
    x - y
  end
end

The rule for a 2-arity primitive application is:

[[ p x y ]] = λκ. [[ x ]] (λa. [[ y ]] (λb. κ (p a b)))

This rule can be extended further for more arguments. Expressing this in Elixir:

# assuming `x` and `y` are in scope here.
fn k1 ->
  (fn k2 ->
    k2.(x)
  end).(fn a ->
    (fn k3 ->
      k3.(y)
    end).(fn b ->
      k1.(a - b)
    end)
  end)
end

Pass this thing the “final continuation” (commonly the identity function Function.identity/1 or, more compactly, & &1), you should see it results in -1 as expected.

A special case is that of 0-arity primitive functions. In that case, we just invoke the function and pass it to the continuation, as if it were a pure value.

node()
# ... becomes simply:
fn k -> k.(node()) end

Lambdas

The next case to consider is how to convert a lambda definition into CPS. To do so, we make it accept a continuation as the first argument, then immediately apply it to a lambda that takes the “original” argument. The body of this inner lambda is another lambda that takes another continuation, with the “CPSed” (converted into CPS) version of the original lambda body fed this inner continuation.

[[ λx. M ]] = λκ1. κ1 (λx. λκ2. [[ M ]] κ2)

Since that is quite convoluted, let’s visualize it by considering the identity function:

fn x -> x end

In CPS, it becomes:

fn k1 ->      # the outer continuation;
  k1.(fn x -> # the argument;
    fn k2 ->  # takes another continuation;
      # then we CPS the body of the original lambda and feed it k2.
      # [[ x ]] k2
    end
  end)
end
# ↓↓↓↓↓↓↓↓↓↓↓↓↓
fn k1 ->
  k1.(fn x ->
    fn k2 ->
      # since it is a irreducible value, we apply the same rules as
      # above.
      (fn k3 ->
        k3.(x)
      end).(k2)
    end
  end)
end

In the above example, one could β-reduce¹¹ the inner lambda and simplify further. But I’ll use this β-expanded version that generalizes better for the cases below¹² .

There is an additional detail about the rule above: if a lambda like the above is directly applied in code, as in (fn x -> x end).(1), then the above conversion is the one use as the CPSed lambda to be applied to 1 (as will be explored later). But if this lambda is returned as a value, one must wrap it in another continuation layer as if it were a pure value:

# the final version of our example, when returned as a value
fn k0 ->        # ← notice the extra continuation `k0`
  k0.(fn k1 ->  # ←
    k1.(fn x ->
      fn k2 ->
        (fn k3 ->
          k3.(x)
        end).(k2)
      end
    end)
  end)
end

I probably have messed something thing up when implementing, but I needed to do this in order for all the thing to behave as expected. I’m curious to know the correct version of this. =)

In case of multiple arguments, we curry the function as in the primitive function application case above before CPSing it with similar rules. As an example that mixes lambda definitions and primitive function applications in its body. The big highlighted area is the CPSed version of the “minus one” shown above.

# [[ fn x, y -> x - y end ]]
#
fn k0 ->                        # ← that extra continuation layer
  k0.(fn k1 ->                  # ─┐
    k1.(fn x ->                 # ─┘ stuff for the `x` argument
      fn k3 ->
        k3.(fn y ->
          fn k4 ->
            (fn k1 ->           # ─┐
              (fn k2 ->         #  │
                k2.(x)          #  │
              end).(fn a ->     #  │ this is the CPSed version of
                (fn k3 ->       #  │ the "minus one" function
                  k3.(y)        #  │ shown above...
                end).(fn b ->   #  │
                  k1.(a - b)    #  │
                end)            #  │
              end)              #  │
            end).(k4)           # ─┘ ... applied to the inner continuation
          end                   #    from the lambda
        end)
      end
    end)
  end)
end

This is already quite unwieldy, and anything more complicated tend to grow quite fast in complexity. A good exercise is to take these more basic examples and try to β-reduce them manually to get more intuition of what-flows-where.

We give the 0-arity case a slightly different treatment: we transform the lambda body, wrap the result in a 0-arity lambda and return that to a continuation.

fn -> :result end
# ... becomes:
fn k0 ->             # again, extra continuation layer
  k0.(fn k1 ->
    k1.(fn ->        # notice that there is no argument here
      fn k2 ->       # ─┐
        k2.(:result) #  │ lambda body converted
      end            # ─┘
    end)
  end)
end

Function application

The last type of terms I’ll attempt to show here is the application of functions to values. The implementation differentiates 3 sub-cases: i) application of values to a lambda literal; ii) application to a named lambda; iii) primitive function application. The last case was already covered above, and it is things of the form fun(x) and Node.ping(). Case (i) is special because we use the converted lambda version without the extra continuation layer. Finally, case (ii) is treated specially because we assume that such function has already been curried and CPSed, so we do not convert it further and simply apply it using the rules that will be shown below.

The conversion rule for an application is:

[[ M N ]] = λκ. [[ M ]] (λm. [[ N ]] (λn. m n κ))

As a final example, we consider the application to a named lambda.

some_fun.(1)
# ... becomes
fn k1 ->
  some_fun.(fn m ->   # ← `some_fun` is considered already CPSed
    (fn k2 ->
      k2.(1)          # ← CPSed argument
    end).(fn n ->
      m.(n).(k1)
    end)
  end)
end

Other details

For more details, I’ll refer the reader to the implementation and to some papers that describe the transformation ^{13 14 15}.

Shift / Reset

Ok, that was quite a lot… Why go through all this trouble?

The answer is that such transformations allow us to use some control operators that are quite powerful. Some examples of applications that can be implemented as libraries are: exceptions, backtracking search, threads, generators and coroutines ¹⁶.

Two of those operators are shift and reset, and there are a few other more or less equivalent ones ¹⁷. They are most succinctly conceptually described in the Racket documentation by the reduction rules:

;; "=>" means "reduces to"
(reset val) => val
(reset E[(shift k expr)]) => (reset (λ (k) expr)
                                    (λ (v) (reset E[v])))
;; where `E` has no `reset`

I have not found in that documentation what E[_] means. But, by experimenting with the operators, it looks like it means the dynamic continuation enclosing the call to shift, up to but not including reset. So, in:

(+ 1
   (reset
    (* 2
       (shift c
         (* 3 (c 4))))))

… E[_] means (λ (v) (* 2 v)). Indeed, the expression above evaluates to 25. Using the second evaluation rule:

(+ 1
   (reset
    ((λ (k) (* 3 (k 4)))
     (λ (v) (* 2 v)))))
;; β-reducing...
(+ 1
   (reset
    (* 3 ((λ (v) (* 2 v)) 4))))
;; using the 1st reduction rule for `reset`...
(+ 1 (* 3 ((λ (v) (* 2 v)) 4)))
;; β-reducing...
(+ 1 (* 3 (* 2 4)))
;; which yields 25

So, shortly, shift captures the continuation and binds it to be used possibly multiple times. The extent of what is capture is determined by the presence of reset, which acts as a delimiter (hence the name delimited continuations).

Just to illustrate, the example above could be written in Elixir as:

x = reset do
      2 * shift cont do
            3 * cont(4)
          end
    end
1 + x

I used an intermediate variable just to emphasize that the “remaining lines” after an expression are continuations for it.

I’ll try to borrow the visualization ideas from those references and attempt to illustrate conceptually how these operators are working in this example (it is almost certainly wrong concretely, I don’t know how Elixir/Erlang break up stack frames). In the images below, each rectangle is a continuation frame, and ● are the places where the redexes go into after being reduced.

When shift is invoked, it essentially captures the frames from the current one up to the nearest enclosing reset, packages those up in cont, and replaces them with its own body frames.

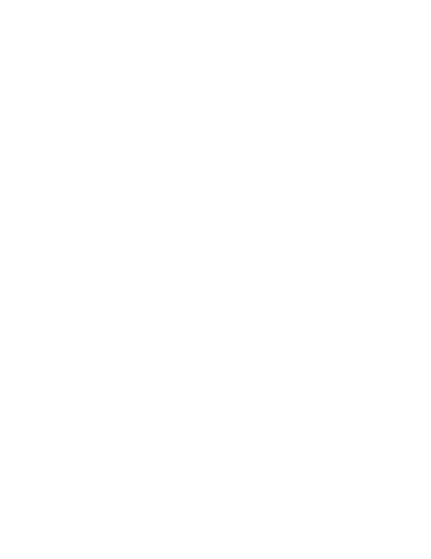
Which reduces to 25, as before.

Footnotes